Pneumatika alapfogalmak
Mi a pneumatika?
A nagynyomású, gázhalmazállapotú közegek műszaki alkalmazásokra felhasználó tudományága. Mivel a pneumatikus eszközök sűrítet levegővel működnek, ezért a továbbiakban úgy definiáljuk, hogy a pneumatika sűrített levegős technológia.
Az ipar főleg automatizálási célokra használja a sűrített levegős technológiát. Ezzel kapcsolatosan pneumatikáról vagy pneumatikus rendszerekről beszélhetünk.
Számunkra a pneumatika a sűrített levegővel történő vezérlést és erőátvitelt fogja jelenteni.
A pneumatika előnyei, hátrányai
A pneumatikus rendszereknek számos előnye van, amelyek közül általánosságban véve a legfontosabbak:
- az energiaforrás, vagyis a sűrített levegő a környezetünkből származik, amely korlátlan mennyiségben áll rendelkezésre
- használat után a sűrített levegő visszanyeri eredeti állapotát, anélkül, hogy bármi változáson menne keresztül
- a sűrített levegő rugalmas, ezért lengés-, és vibráció-csillapításnál, rugózásnál előnyösen alkalmazható
- a sűrített levegő csővezetékeken keresztül gyorsan szállítható anélkül, hogy jelentős veszteségek lépnének fel
- felhasználható olyan területeken is, ahol fokozott a tűz- és robbanásveszély
- a nyomás-, és mennyiség-szabályozásnak köszönhetően az energiaátvitel tág határok között szabályozható
- a pneumatikus elemek könnyen szerelhetők, karbantarthatók, működésük megbízható
Az előnyök mellett a legjellemzőbb hátrányokkal is szembesülnünk kell:
- a sűrített levegő - a felhasználás helyétől függően - gondos előkészítést igényel, mivel a környezeti levegő kompresszálását követően nedvességet, valamint szilárd és légnemű szennyeződést is tartalmazhat
- a sűrített levegő előállítása a magas energiaárak, valamint a kompresszorok hatásfoka miatt viszonylag drága energiahordozó
- a levegő összenyomhatóságából adódóan nem lehet a végrehajtóelemek terhelés- független pozícionálását megvalósítani
Fizikai alapfogalmak, mértékegységek
Az SI mértékegységrendszer számos alap és származtatott mértékegységre épül.
[Mértékegységek Nemzetközi Rendszere, röviden SI(Systeme International d'Unités)]
Alap mértékegységek, amelyek számunkra - a pneumatikában - érdekesek lehetnek:
- méter - m (hossz)
- kilogramm - kg (tömeg)
- másodperc - s (idő)
- kelvin - K (hőmérséklet)
Származtatott mértékegységek, amelyet tisztázunk:
- newton - N (erő)
- pascal - Pa (nyomás)
Erő
Azokat a hatásokat, amelyek a testeken alak-, vagy mozgásállapot-változásokat hoznak létre, erőhatásoknak nevezzük. Azt a fizikai mennyiséget, amely a testek közötti kölcsönhatást (erőhatást) jellemzi, erőnek nevezzük.
A fizikában az erő olyan hatás, amely egy tömeggel rendelkező testet gyorsulásra késztet.
jele: F
mértékegysége: newton
mértékegységének a jelölése: N
SI-ben kifejezve:
![]() (kilogramm * méter / szekundum-négyzet)
(kilogramm * méter / szekundum-négyzet)
Nyomás
A nyomás fizikai mennyiség, az anyagok egyik fizikai jellemzője, állapothatározó. A nyomás a folyadékokban és gázokban egyformán terjed minden irányban. A nyomást a nyomóerő (F) és a nyomott felület (A) hányadosából számítjuk ki, vagyis
jele: p
mértékegysége: pascal
mértékegységének a jelölése: Pa
SI-ben kifejezve:
![]() (newton / négyzetméter)
(newton / négyzetméter)
A nyomás esetén a következő többszörösüket szokás használni:
1 kPa (kilopascal) = 1.000 Pa
1 MPa (megapascal) = 1.000.000 Pa
A bar elnevezés használata általánosan elterjedt a fluidtechnikában.
1 bar = 100.000 Pa = 0,1 MPa = 0,1 N/mm2 (newton / négyzetmilliméter)
Néhány országban, így például Nagy-Britanniában és az Egyesült Államokban használatos még
a psi (font / négyzethüvelyk)
1 psi = 0,07 bar, kerekítve
A normál légköri nyomás, a tengerszintre vonatkoztatott nyomás, melynek értéke 1 atm (atmoszféra).
1 atm = 101.325 Pa = 1013,25 mbar (millibar) vagy hPa (hektopascal)
Ezt a mértékegységet elsősorban a meteorológiában használják. A gyakorlatban 1 atm = 1 bar.
A túlnyomás a normál légköri nyomás fölötti értéket mutatja. Az abszolút nyomás értékébe a légköri nyomást is beleszámítjuk, tehát az abszolút nyomást 0 Pa-tól számoljuk.
abszolút nyomás = túlnyomás + légköri nyomás.
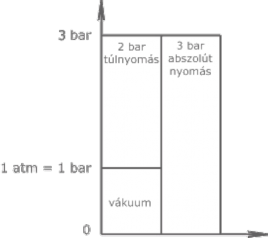
Jelölések összefoglalása
- p(a) : abszolút nyomás
- p(t) : túlnyomás
- -p(t) : vákuum
Példák
- 6 bar túlnyomás = 6 bar(t)
- 7 bar abszolút nyomás = 7 bar(a)
- 0,7 bar abszolút nyomás = 0,7 bar(a) vagy -0,3 bar(t)
A túlnyomás és a vákuum elnevezés arra utal, hogy a nyomás nagyobb vagy kisebb, mint a légköri nyomás.
A vákuum minőségét osztályokra szokták bontani:
Vákuum osztályozása
| Normál légköri nyomás | 101 325 Pa | = 1,01325 bar = 1 bar |
| Elő vákuum (vagy "durva vákuum") | 100 kPa ... 3 kPa | = 1 bar ... 0,03 bar |
| Közép vákuum | 3 kPa ... 100 mPa | = 0,03 bar ... 0,001 mbar |
| Nagy vákuum | 100 mPa ... 1 µPa | = 0,001 mbar ... 0,01 nbar |
| Ultra nagy vákuum | 100 nPa ... 100 pPa | |
| Extrém nagy vákuum | < 100 pPa | |
| Világűr | 100 µPa ... < 3 fPa | |
| Tökéletes vákuum | 0 Pa |
A pneumatikában a bar mértékegység használatos.
Ha nincs egyéb utalás rá, akkor a nyomás alatt túlnyomás értendő.
Lássuk ezt a gyakorlatban...
Számítsuk ki, hogy mekkora erőt fejt ki egy adott méretű munkahenger, adott nyomáson.
Pascal törvénye értelmében:
![]()
p: nyomás [Pa]
F: erő [N]
A: felület [m2]
Mekkora erőt fejt ki egy 40 mm átmérőjű munkahenger, 6 bar nyomáson, ha alaphelyzetéből indulva a véghelyzetbe működtetjük?
Azért hogy az értékeketmértékegység-helyesen helyettesítsük be a képletekbe, a nyomásértéket átváltjuk MPa-ba, amely nem más, mint N/mm2, a hosszméreteket pedig mm-ben adjuk meg.
Munkahenger átmérője:
Amely a tulajdonképpen a munkahenger dugattyújának az átmérője:
![]()
A munkahenger dugattyújának a felülete:
A kör területének a számítása, azaz a kör keresztmetszetű munkahenger dugattyújának a felülete:
![]()
A képletbe behelyettesítve az értékeket:
![]()
Üzemi nyomás:
![]()
A munkahenger nyomóerejének a számítása:
Pascal törvénye értelmében:
![]()
A képletbe behelyettesítve az értékeket:
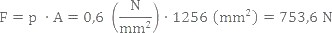
A kiszámolt érték egy elméleti erő. A gyakorlatban 5% veszteséggel számolhatunk, amely a súrlódást, valamint az egyéb veszteséget korrigálja.
Ennek megfelelően egy 40 mm átmérőjű munkahenger, 6 bar nyomáson megközelítőleg 716 N nyomóerőt fejt ki, amely - gyakorlatias szemmel nézve - egy közel 73 kg-os tömeg súlyerejének felel meg.
Mekkora erőt fejt ki ugyanez a munkahenger, ha véghelyzetből alaphelyzetbe működtetjük?
Ugyanennek a munkahengernek a húzóereje kisebb, mint a nyomóereje, mivel a dugattyúrúd által lefedett területre a munkahenger dugattyúján nem hat a levegő nyomása.
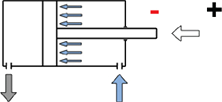
A dugattyú felületének számításakor a dugattyúrúd által csökkentett felületet vesszük figyelembe.
(Azaz a dugattyú által meghatározott kör területéből kivonjuk a dugattyúrúd által meghatározott kör területét.)
D = dugattyú átmérője (40 mm)
d = dugattyúrúd átmérője (16 mm)
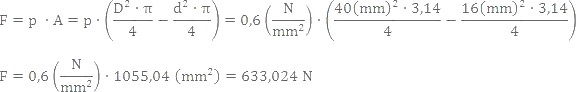
Az 5% veszteséggel való számolást követően a munkahenger húzóereje megközelítőleg 601 N, szemben a 716 N nyomóerővel.
A következő fejezetben a pneumatikus rendszer alapvető elemeit tekintjük át.



